Das Modell
Wie bereits im einführenden Kapitel beschrieben gibt es im Exmouth-Golf zahlreiche Mangrovenwälder. Mithilfe von MANGA wird die Wachstumsdynamik der Mangroven in einem Modell abgebildet. Hauptaugenmerk liegt dabei auf der für Mangrovenwälder typischen Struktur und die Dominanz einzelner Mangrovenarten unter verschiedenen Standortbedingungen. Neben dem Wachstumsverhalten der Mangroven wird die Salinität des Bodenwassers - auch als eine sensitive Einflussgröße auf das Wachstum - genauer betrachtet. Dabei werden die wechselwirkenden Einflüsse des Mangrovenwachstums und der Gradienten der Salinität im Bodenwasser berücksichtigt. In diesem Kapitel wird der Aufbau des Modells, die Grundlagen der Modellierung mit MANGA und die Ergebnisse der Arbeit beschrieben.
Modellgebiet
Im Modell wird ein Transekt von 185 m Länge und 10 m Breite abgebildet (Abbildung 1). Zur Evaluierung der Modellergebnisse werden sowohl Allometriedaten aus einer Transektenmessung, als auch Messergebnisse einer Langzeitstudie verwendet. In der Langzeitstudie werden die Auswirkungen von Düngung auf das Wachstum von insgesamt 72 Mangroven, von denen jeweils die Hälfte an der land- und an der seeseitigen Seite des Transekts steht, dokumentiert (siehe auch die in Abbildung 4 eingezeichneten „Treatment Averages“).
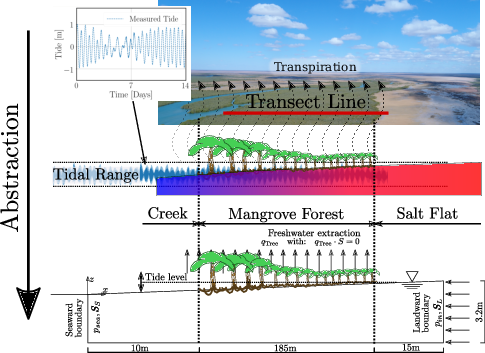
Das Modell bildet das Mangrovenwachstum an der in nachfolgender Darstellung zu sehenden Stelle im Exmouth-Golf dar.
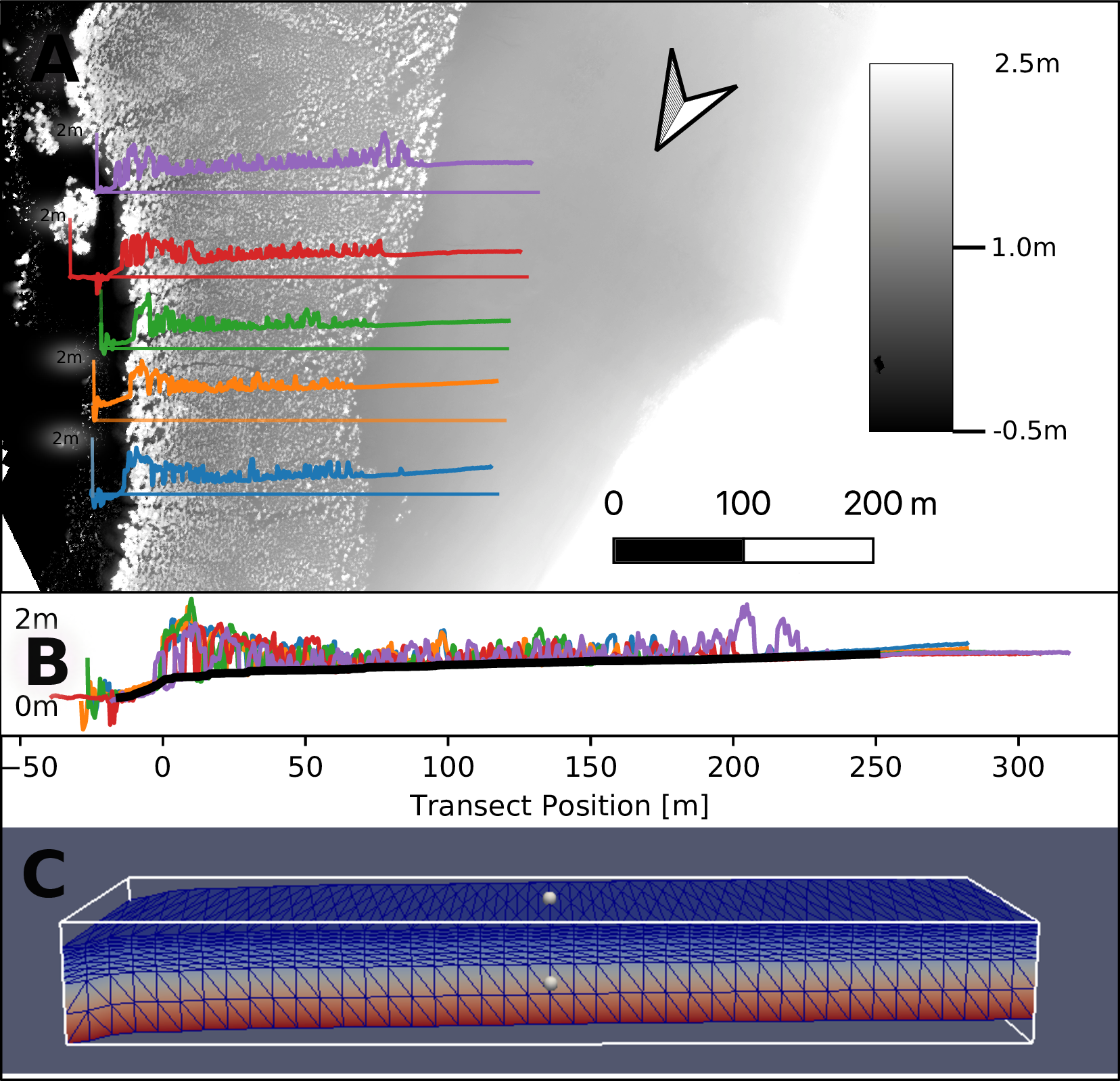
Die Höhenprofile aus dem digitalen Oberflächenmodell der fünf Transekte (Abbildung 2 A) wurden übereinander gelegt und aus den fünf Signalen (Abbildung 2 B) die Geländeoberkante aus der Grundlinie der Signale interpoliert (Abbildung 2 C). Das so entstehende DGM wurde für die Diskretisierung des Grundwassermodells genutzt.
Modellierung
Modellvarianten
Das Mangrovenwachstum wurde mit Hilfe von drei verschiedenen Modellen simuliert (siehe auch Tabelle 1).
Im Modell „Model Without Feedback“ werden die dynamischen Veränderungen der abiotischen Einflüsse (Gezeiten, Grundwasserneubildung und Salzgehalt des Meerwassers) über entsprechende Randbedingungen berücksichtigt. Der Einfluss der Pflanzenwasserentnahme auf den Salzgehalt des Porenwassers wurde nicht abgebildet.
Das Modell „Model Without Tide“ berücksichtigt die Auswirkungen der Pflanzenwasserentnahme auf den Salzgehalt des Porenwassers und alle abiotischen Einflüsse des ersten Modells – mit Außnahme der Gezeiten.
Die dritte Modellvariante „Full Model“ bildet schließlich sowohl die Dynamik der Gezeiten als auch die Kopplung der Pflanzenwasserentnahme und des Porenwassers ab.
Nachfolgende Tabelle 1 fasst die Spezifikationen der drei Modellvarianten zusammen.
| Gezeiten | Kopplung Pflanzenwasserhaushalt und Porenwasser | Sonstige abiotische Faktoren | |
| Model Without Feedback | ✔ | ✘ | ✔ |
| Model Without Tide | ✘ | ✔ | ✔ |
| Full Model | ✔ | ✔ | ✔ |
Diskretisierung
Grundwassermodell
Das Grundwassermodell bildet den Untergrund mit einem Gitter der Ausmaße 10 m x 230 m x 3 m auf fünf FEM-Layern mit insgesamt 5880 Zellen ab. Nachfolgende Abbildung 3 zeigt die räumliche Diskretisierung aus seeseitiger Perspektive.
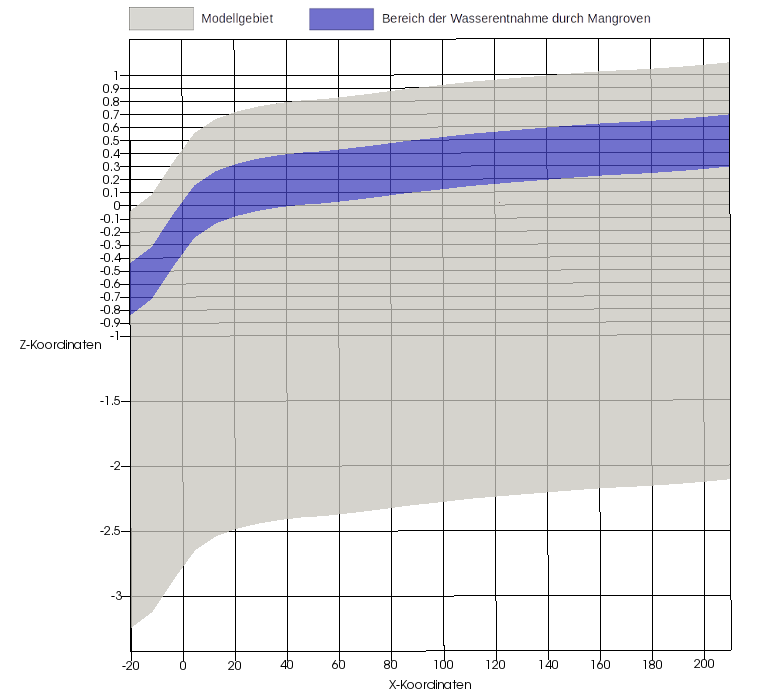
Die Mangroven entnehmen dem Untergrund Bodenwasser aus einer Tiefe von 40 cm bis 80 cm unter der Geländeoberkante. Abbildung 4 zeigt das Modellgebiet (Grau) und den Bereich der Wasserentnahme durch die Mangroven (Blau). Zu beachten ist die 50-fache vertikale Skalierung.
Zeitlich diskretisiert wird das Grundwassermodell mit einer Zeitschrittlänge von einer Stunde. Der Tidenhub als dynamische Randbedingung wird mit der Zeitreihe der Jahre 1991 bis 1993, die über die gesamte Modelllaufzeit immer wieder wiederholt wird, abgebildet.
Baumwachstumsmodell
Da jede Mangrove als einzelnes Individuum abgebildet wird findet eine räumliche Diskretisierung im eigentlichen Sinne nicht statt. Zeitlich wird das Baumwachstumsmodell mit einer Zeitschrittlänge von einem halben Jahr (1 a = 365.25 d) diskretisiert.
Randbedingungen Grundwassermodell
Der Salzgehalt des Meerwassers wurde mit 50 g/kg festgelegt, das Bodenwasser am landseitigen Ende des Transsekts bekam eine Salinität von 70 g/kg zugewiesen. Durch die Transpiration der Mangroven erhöhen diese lokal den Salzgehalt im Porenwasser. Der Wasserstand wird in Form des hydrostatischen Drucks an der see- und landseitigen Kante des Modellgebiebts bestimmt. Zur Abbildung der Gezeiten wurde der seeseitige Wasserstand dabei als dynamische Randbedingung 1. Art in das Modell integriert. Als Datengrundlage dienen hier die Wasserstandsmessungen des Department of Transport der Government of Western Australia. Der landseitige Wasserstand wird über eine konstante Randbedingung 1. Art abgebildet. Die Evapotranspiration der Bäume wird durch Senken im Bereich der Wurzeln abgebildet (vgl. Abbildung 4). Zufluss in Form von Niederschlag wird indirekt über den Salzgehalt am landseitigen Rand des Modellgebiets berücksichtigt. Die hier nicht erwähnten Modellränder werden alle als No-Flow-Randbedingungen definiert. Eine schematische Übersicht des Modellgebiets stellt auch Abbildung 1 dar.
Parametrisierung
In den nachfolgenden Tabellen finden sich die Parametrisierungen des Untergrunds (Tabelle 2) und der Mangroven (Tabelle 3), globale Gewichtungsfaktoren (Tabelle 4) sowie die Anfangswerte der Geoemtrieen der Mangrovensetzlinge (Tabelle 5).
Untergrund
Botanik
Wasserhaushalt der Mangroven
Globale Gewichtungsfaktoren
Anfangswerte der geometrischen Kennwerte für Mangrovensetzlinge
Ressourcenkonkurrenz
Um die Mangroven im Modellgebiet abzubilden, bedarf es der Herstellung einer stabilen Population, also dem Erreichen von quasi-stationären Verhältnissen. Hierzu werden zunächst 30 Mangroven zufällig im Modellgebiet als Setzlinge positioniert. In jedem Zeitschritt (Länge: halbes Jahr) kommen nun 30 neue Mangroven hinzu, die ebenfalls zufällig im Modellgebiet positioniert werden. Aufgrund des wettbewerbsbasierten Baumwachstumsmodells sterben diese neuen Mangroven mehr oder weniger schnell wieder ab. So ist die Wahrscheinlichkeit, dass eine junge Mangrove im Einzugsgebiet einer bereits älteren sehr schnell wieder stirbt sehr hoch. Ursächlich hierfür ist die überirdische Konkurenz betreffend vor allem das fehlende Sonnenlicht. Durch die Aufkonzentrierung des Salzgehalts, bedingt durch die Entnahme von Frischwasser der anderen Mangroven, entstehen im Porenwasser Salzfahnen. Diese sorgen für schlechtere Wachstumsbedingungen der sich im Abstrom befindenden (jungen) Mangroven. Unterschiedliche Mangrovenarten haben eine jeweils höhere oder niedrigere Toleranz gegenüber hohen Salzkonzentrationen. In dieser Arbeit wurden in diesem Zusammenhang die beiden Arten Avicennia marina („graue Mangrove“) und Rhizophora mangle („rote Mangrove“) genauer betrachtet.
Ergebnisse
In dieser Arbeit wurden mit Hilfe des MANGA-Modells zwei Prozesse genauer betrachtet. Zum einen sollte die Entwicklung der typischen Strukturen in Mangrovenwäldern abgebildet werden, zum anderen sollte das Wachstumsverhalten der beiden Mangrovenarten unter verschiedenen Umweltbedingungen Untersucht werden. Im nachfolgenden werden die Ergebnisse kurz zusammengefasst.
Waldstruktur
Nachfolgende Visualisierung zeigt die dynamische Entwicklung der Mangrovenpopulation im Modellgebiet und die Entwicklung der Biomasse. Gut nachvollziehbar ist hier, bereits in den ersten 100 Zeitschritten, die immer stabiler werdende Mangrovenpopulation. Es bilden sich relativ schnell Bereiche über die X-Länge des Transsekts aus, in denen große und somit Mangroven die sehr alt werden wachsen, und solche, in denen junge Mangroven schnell wieder sterben. Dadurch, dass in jedem Zeitschritt 30 neue Mangroven als Setzlinge in das Modell hinzukommen und die Nährstoffkonkurenz anfangs sehr gering ist, wächst die Biomasse im Modell zunächst sehr stark an. Mit steigender Anzahl an Mangroven im Modellgebiet wird die Konkurenz zwischen den einzelnen Bäumen immer größer. Nach dem globalen Maximum der Biomasse fällt diese durch für einige Mangroven immer schlechter werdende Nährstoffbedingungen zunächst wieder leicht ab. Nach einer gewissen Zeit stellt sich dann ein quasi-stationärer Zustand der Mangrovenpopulation ein.
Im nachfolgenden Video wurde das Modellgebiet in zehn Sektoren unterteilt. Dargestellt wird die dynamische Entwicklung der Mangrovenpopulation und der Salzkonzentration im Bodenwasser sowie die Biomasse der Mangroven in den einzelnen Sektoren. Im Vergleich zur vorhergehenden Visualisierung ist in diesem Video eine Hauptursache der Ausbildung der typischen Waldstruktur zu erkennen, nämlich die Aufkonzentrierung des Salzgehalts im Bodenwasser durch Transpirationsprozesse der Mangroven. Die hohe Korrelation zwischen Salzkonzentration und Biomasse in den einzelnen Sektoren ist bereits ab einer Modelllaufzeit von 40 Jahren zu erkennen. Bereits ab 100 Jahren ist die sich langsam ausbildende, für Mangrovenwälder typische, Struktur erkennbar.
Die Ergebnisse des „Full Models“ stimmen mit den gemessenen Felddaten qualitativ überein (Abbildung 5). Dies trifft sowohl auf das Baumhöhenprofil (Abbildung 5 A) als auch auf das Profil des Salzgehalts des Porenwassers (Abbildung 5 B) in dem untersuchten Transekt zu. Insbesondere die Variation des Porenwassersalzgehalts konnte gut abgebildet werden (Abbildung 5 A). Das Bestimmtheitsmaß der Bravais-Pearson-Korellation beträgt für die Baumhöhe R² = 0,64 und für die Salinität des Porenwassers R² = 0,88. Ein Vergleich der Ergebnisse des „Full Models“ mit den Ergebnissen der beiden Modellvarianten „Model Without Feedback“ und „Model Without Tide“ zeigt eine deutlich schlechtere Wiedergabe der gemessenen Felddaten durch die beiden einfacheren Modelle (Abbildung 5 C und 5 D).
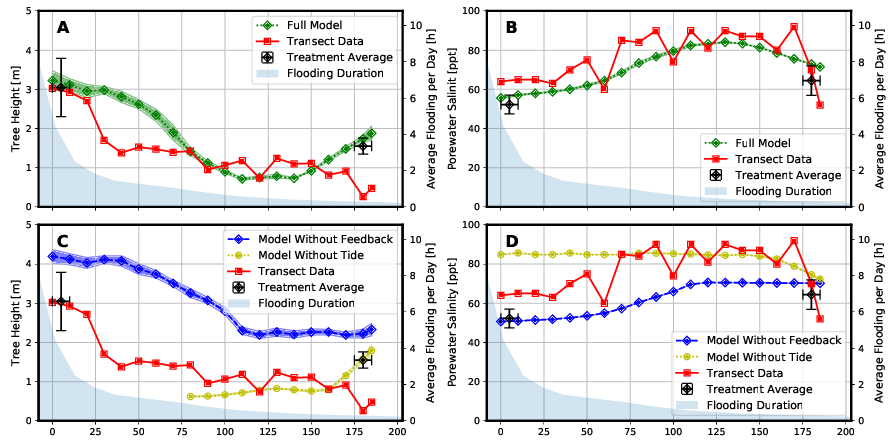
Die in der Abbildung 5 eingezeichneten „Treatment Averages“ sind zwei Bereiche, in denen schon seit längerer Zeit die dort wachsenden Mangroven genauer untersucht werden. Ein Vergleich der Ergebnisse dieser Beobachtungen mit den Ergebnissen der Modellierung zeigt ebenfalls eine hohe Übereinstimmung.
Um die Auswirkungen der Berücksichtung der zeitlichen Dynamik der Gezeiten und der Pflanzenwasserentnahme auf den Salzgehalt im Porenwasser zu untersuchen, wurde diese mit folgender Formel normiert:
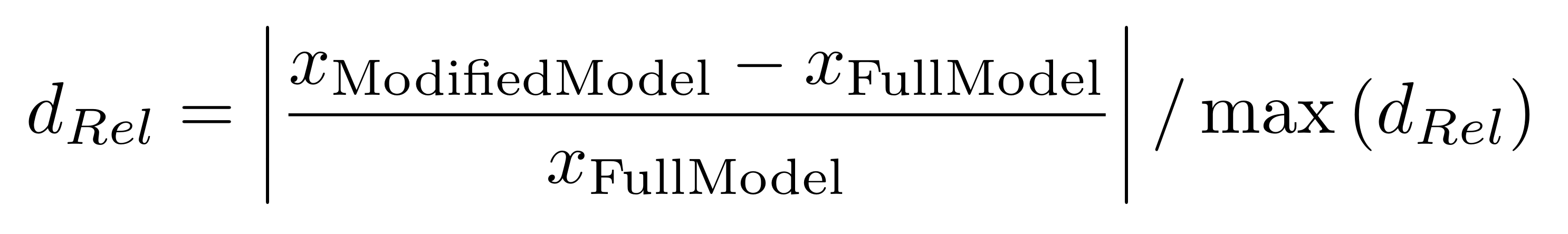
Diese relativen Auswirkungen sind in nachfolgender Abbildung 6 für die Baumhöhe und den Porenwassersalzgehalt abgebildet. Ein Wert von Null würde bedeuten, dass sich die Ergebnisse zwischen Full Model und dem jeweiligen vereinfachtem Modelltyp nicht unterscheiden. Je größer der Wert wird, umso höher ist die Abweichung.
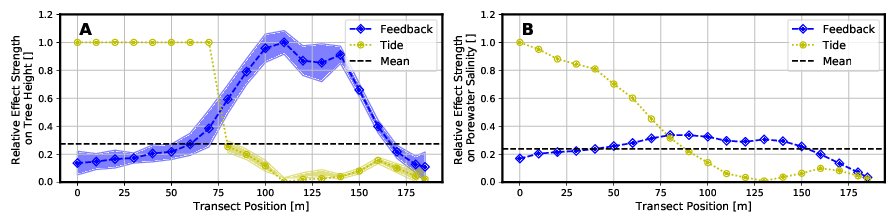
Aufgrund der größeren Auswirkungen des Tidenhubs im seenahen Bereich kann das Modell „Without Tide“ sowohl die Bäumhöhen als auch den Porenwassersalzgehalt hier nur mit relativ großer Abweichung im Vergleich zum „Full Model“ abbilden. Je weiter man sich aber in Richtung Festland bewegt, desto geringer werden die Wasserstandsschwankungen aufgrund der Gezeiten. Die Baumhöhen und Salzgehalte können in diesem Bereich (x > 75 m) mit geringeren relativen Abweichungen zum „Full Model“ abgebildet werden.
Das Modell „Without Feedback“ hat insbesondere im mittleren bis landseitigem Bereich (60 m < x < 165 m) des Transsekts Probleme, die Wachstumshöhe der Mangroven so abzubilden, wie es das „Full Model“ macht. In diesem Bereich kommt es zur Aufkonzentrierung der Salinität des Bodenwassers durch die Pflanzenwasserentnahme, welche in diesem Modelltyp aber nicht abgebildet wird.
Speziendominanz
Im vorangegangenem Abschnitt wurde gezeigt, dass MANGA mit der Berücksichtigung von Salzkonzentration im Bodenwasser und des Tidenhubs in der Lage ist, die für Mangrovenwälder typischen Waldstrukturen abzubilden. Mit Hilfe der umfangreichen Parametrisierungsmöglichkeiten des Baumwachstumsmodells (siehe hierzu auch den Abschnitt Parametrisierung) kann mit MANGA auch das Wachstum einzelner bestimmter Individuenarten untersucht werden. Verschiedene Mangrovenarten zum Beispiel weisen verschiedene Toleranzen gegenüber zu hohen Salzgehalten auf. In diesem Projekt wurde das Wachstumsverhalten der beiden Arten Avicennia marina („graue Mangrove“) und Rhizophora mangle („rote Mangrove“) genauer betrachtet.
Abbildung 7 zeigt die Speziendominanz dieser beiden Mangrovenarten bei unterschiedlichen Salzkonzentration (siehe Tabelle 6) im Bodenwasser. Die verschiedenen in der Abbildung dargestellten Setups unterscheiden sich nur hinsichtlich der Randbedingungen der seeseitigen und landseitigen Salzkonzentrationen des Bodenwassers. Für die Betrachtung der Speziendominanz im Modellgebiet wir die Speziendominanz d eingeführt und wie folgt definiert:
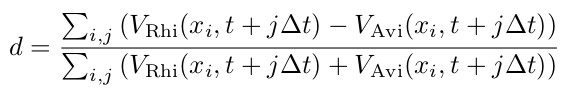
Vi(x,t) stehen hierbei für das Volumen der im betrachteten Zeitschritt (t) und X-Koordinatenabschnitt (x) vorhandenen Mangrovenarten Rhizophora mangle (VRhi(x,t)) und Avicennia marina (VAvi(x,t)).
| Setup | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| seeseitige Salinität [g/kg] | 15 | 15 | 25 | 50 | 50 | 35 |
| landseitige Salinität [g/kg] | 25 | 40 | 55 | 60 | 45 | 35 |
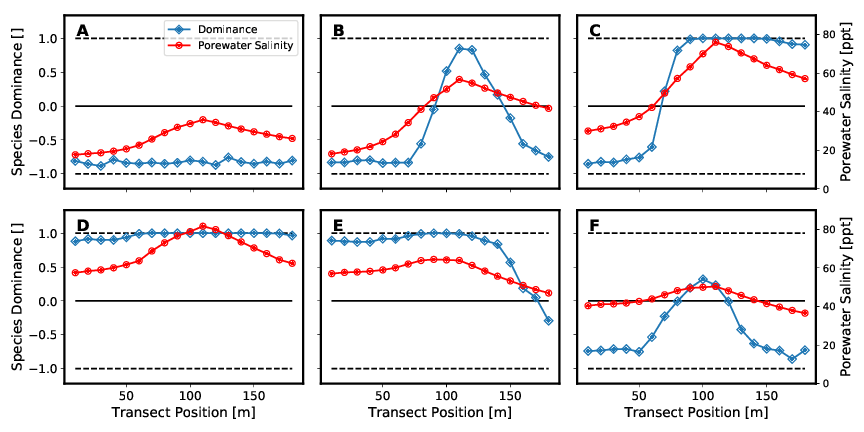
Dabei zeigen die Abb. 7A bis 7D einen zunächst bedingt durch sowohl seeseitige sowie landseitige niedrigen Salzkonzentrationen monospezifischen Rhizophora-Wald (Abb. 7A). Mit steigender Salinität stellt sich ein Mischwald aus beiden Arten ein (Abb. 7B und 7C). Abb. 7D bildet dann aufgrund der hohen Salzkonzentrationen einen monospezifischen Avicennia marina Wald ab. Die beiden Abb. 7E und 7F sind den Setup-Konfigurationen Abb. 7B und 7C dahingehend ähnlich, dass die Werte der Salinitäten an land- bzw. seeseitiger Seite des Transsekts in etwa den jeweils anderen Wert annehmen. Auch sie bilden somit einen Mischwald aus beiden Arten ab. Diese Ergebnisse werden in folgender Abbildung 8 noch einmal auf eine andere Art dargestellt.
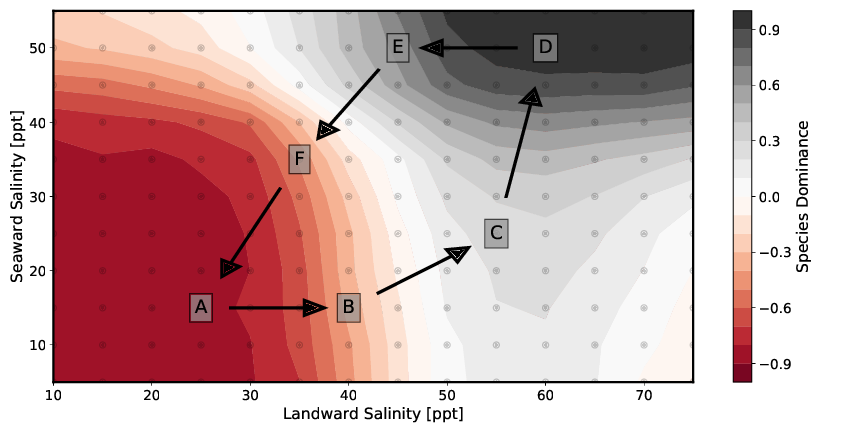
Bei der Betrachtung der Mischwälder fällt auf, dass sich nur in einzelnen Abschnitten wirkliche Mischpopulationen einstellen. In den meisten Bereichen bildet sich eine eindeutige Dominanz einer Spezienart. Diese scharfen Übergänge zwischen den einzelnen Dominanzzonen zeigen, dass eine Koexistenz zwischen den verschiedenen Arten nur in Bereichen bestimmter Porenwassersalinitäten möglich ist. Die Lage der Grenzen und die Änderung der Speziendominanz d (Steigung der Kurve) hängen von den individuenspezifischen Parametern im Baumwachstumsmodell ab. Zu Beachten ist hier, dass der Salzgehalt im Bodenwasser auch durch die Individuenanzahl pro Fläche und die Baumhöhen beeinflusst wird. Diese beiden Kennwerte werden wiederum von eben jenen individuenspezifischen Parametern beeinflusst.
Die Kopplung zwischen Pflanzenwasserhaushalt und Porenwasser beeinflusst folglich die Ausbildung der Waldstruktur maßgeblich. In den Setups die zur Ausbildung eines Mischwaldes führen entstehen entweder zwei- (siehe Abbildungen 7C und 7E) oder dreizonige (siehe Abbildungen 7B und 7F) Mischwälder. Die beiden Zonen an see- und landseitigem Modellrand werden dabei maßgeblich durch die Parameter der Salinität als Randbedingung definiert. In der Modellmitte kommt es durch die Transpiration der Mangroven zu einer Aufkonzentration des Porenwassersalzgehalts. Überschreitet diese einen gewissen Wert, dominiert die salzresistentere Art Avicennia marina.
Wie auch in Abbildung 9 dargestellt, stimmen die Ergebnisse der Betrachtung der Speziendominanz im Modell mit den gemessenen Felddaten in denen im Projekt betrachteten Transsekten überein.
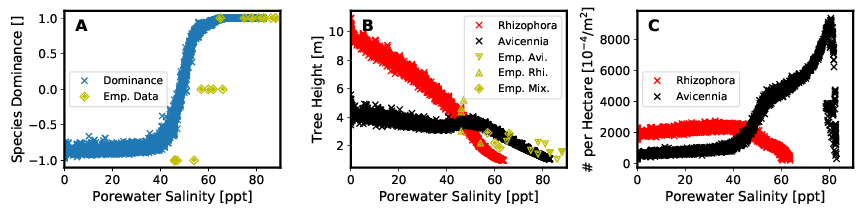
Die Modellsoftware MANGA ist folglich in der Lage nicht nur die sich entwickelnde Struktur eines Mangrovenwaldes abzubilden, sondern auch dessen Zusammensetzung aus verschiedenen Spezien.
Fazit
Mit Hilfe des „Full Models“ konnte die für Mangrovenwälder typische Struktur abgebildet werden. Konkret konnte die Waldstruktur des Avicennia marina Monokulturwalds im betrachteten Gebiet im Exmouth-Golf in Western Australia mit den zur Verfügung stehenden Felddaten auf eine übereinstimmende Weise reproduziert werden. Die Abweichungen der Baumhöhen und des Salzgehalts des Bodenwassers zwischen Modell und gemessenen Werten liegen im Bereich der Variablität der Feldmessungen. MANGA ist hierzu auch ohne weitere Kalibrierung der pflanzenspezfischen Parameter in der Lage. Im „Full Model“ konnten Bereiche im Modellgebiet erkenntlich gemacht werden, in denen entweder die Gezeiten oder die Vegetation die Struktureigenschaften maßgeblich beeinflusst.
Aufgrund der Ergebnisse der Modellierung muss davon ausgegangen werden, dass eine korrekte Abbildung des Mangrovenwachstums mit MANGA nur unter Berücksichtigung des Tidenhubs und der Einflüsse der Wasserentnahme der Mangroven aus dem Untergrund möglich ist. Eine Kalibrierung der Pflanzenparameter ist hierfür nicht notwendig. Ebenfalls nicht berücksichtigt werden Heterogenitäten hydrogeologischer Eigenschaften des Untergrunds, z.B. die hydraulische Leitfähigkeit oder Porosität betreffend.
Die durch die Pflanzenwasserentnahme verursachten Gradienten der Salzkonzentration im Bodenwasser wirken sich vor allem im landseitigen Bereich signifikant auf die Wachstumsdynamik der Mangrovenpopulation aus. Weiter lässt sich aus den Ergebnissen schließen, dass der Einfluss der Gezeiten ein Haupteinflussfaktor auf die Gradienten der Salzkonzentration im Bodenwasser ist. Dieser Einfluss ist am seeseitigen Ende des Transsekts am größten. Mit sinkender Höhe der Flut, bzw. kleinerer Überflutungsdauer, nimmt die Rückkopplung zwischen Pflanzenwasser- und Bodenwasserhaushalt dabei eine immer größere Bedeutung an.
Mit Hilfe der Sensitivtätsanalyse des Modells hinsichtlich der Speziendominanz konnte gezeigt werden, dass die Artenzusammensetzung durch die gekoppelte Betrachtung von Bodenwasserhaushalt und Pflanzenwasserentnahme über die Systemgrenze hinweg beschrieben werden kann. Durch die Variation von nur zwei Parametern (vgl. Tabelle 3), die sich direkt auf die Wasseraufnahme der Bäume auswirken, konnten typische Zonierungsmuster in Mangroven-Mischwäldern reproduziert werden. Dies gelang auch mit nur grob geschätzten pflanzenspezifischer Parameter für eine der beiden Arten. Werden die Randbedingungen der Salzkonzentrationen an land- und seeseitiger Seite beide sehr hoch oder sehr niedrig gewählt bilden sich überwiegend Wälder aus Monokulturen aus. Wählt man einen moderaten Mittelwert der Salinitäten bilden sich Mischwälder aus beiden Arten. Diese weisen Zonen mit klarer Dominanz einer Art auf, die durch scharfe Übergänge getrennt sind. Diese Übergänge hängen dabei nachweislich vom Bodendwassersalzgehalt ab. Die Spezienzusammensetzung im Modell stimmt mit den gemessenen Felddaten überein.
Ausblick
In der Literatur gibt es Hinweise darauf, dass sich Mangroven über die Zeit an ihre Umweltbedingungen anpassen. Eine niedrigere Salzkonzentration im Bodenwasser sorgt für eine höhere Xylemleitfähigkeit und damit für eine größere Transpiration. Gleichzeitig sorgt eine geringe Salzkonzentration im Untergrund aber auch für höhere Blattwasserpotentiale, die die Transpiration hemmen. Diese sich gegenseitig ausgleichenden Prozesse sorgen für insgesamt etwa gleichbleibende Transpirationsraten bei unterschiedlichen Salinitäten des Porenwassers. Eine genauere Betrachtung dieser Prozesse kann dabei helfen, die Fähigkeit der Mangroven ihre Physiologie an entsprechenden Standorten vorherrschende Umweltbedingungen anzupassen detailiert zu untersuchen.
Der Niederschlag wurde in diesem Projekt, wie bereits weiter oben beschrieben, nicht dynamisch und als eigener Prozess integriert, sondern über die landseitige konstante Randbedingung des Wasserstands und Salzgehalts abgebildet. Der Exmouth-Golf ist im Allgemeinen eine Region mit sehr niedrigen Jahrsniederschlagssummen. Die Variabilität der einzelnen Regenereignisse ist jedoch sehr hoch. Durch Zyklone kommt es regelmäßig zu ausgeprägten Starkregenereignissen, die einen nicht unerheblichen Anteil an der Gesamtsumme des Niederschlags ausmachen. Der Einfluss des Niederschlags auf die Mangrovenpopulation wurde indirekt durch das Setzen unterschiedlicher Werte der Randbedingung der landseitigen Porenwassersalinität untersucht. Da sich diese Randbedingung als sehr sensitive Größe gezeigt hat, folgt daraus, dass auch der Niederschlag einen Einfluss auf die Zusammensetzung der Mangrovenarten und im Allgemeinen die Ausbildung der typischen Mangrovenwaldstrukturen hat. Im Zuge des Klimawandels ist davon auszugehen, dass Starkregenereignisse bzw. Extremwettersituationen im Allgemeinen zunehmen werden und der Meeresspiegel ansteigt. Da das Modell in der Lage war, die Populationen der Realität entsprechend abzubilden, könnte es auch dafür verwendet werden die Auswirkungen des Klimawandels auf die empfindlichen Ökosysteme der Mangrovenwälder zu untersuchen. Weiter kann das Modell wichtige Hinweise bei der Untersuchung sämtlicher Zusammenhänge zwischen Waldstrukturen und Pflanzenmerkmalen liefern. Modelle, die die Prozesse auf konzeptionelleren Ansätzen basierend abbildet als es bei MANGA der Fall ist, können mit letzterem kalibriert und verifiziert werden.

